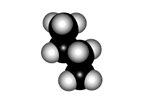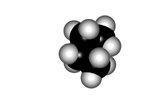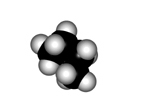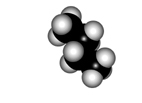
The atoms bonded by a single bond rotate one with respect to the other at a very low energy cost.
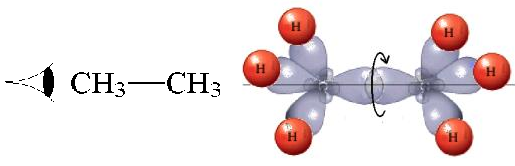
In ETHANE the C-C bond is the consequence of the frontal overlapping of two hybrid sp3 orbitals.
Let's use as an axis the imaginary line passing through the two bonded atoms.
It is pretty intuitive that if one twists one hybrid orbital relative to the other, around the aforementioned axis, their overlapping does not vary at all and therefore, the bond does not suffer any erosion with the twisting
The number of possible conformations (rotamers) around a single bond is infinite.
However, we can tell apart two signifficant positions:
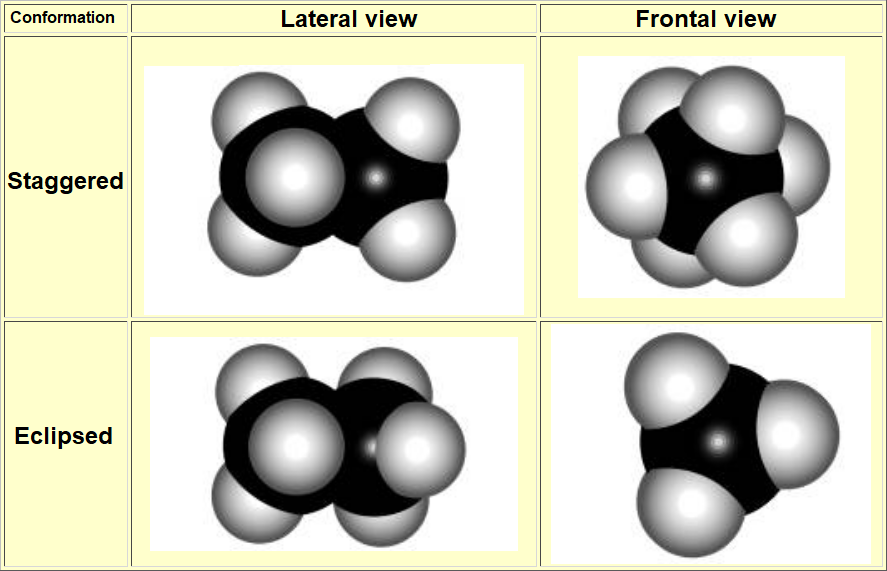
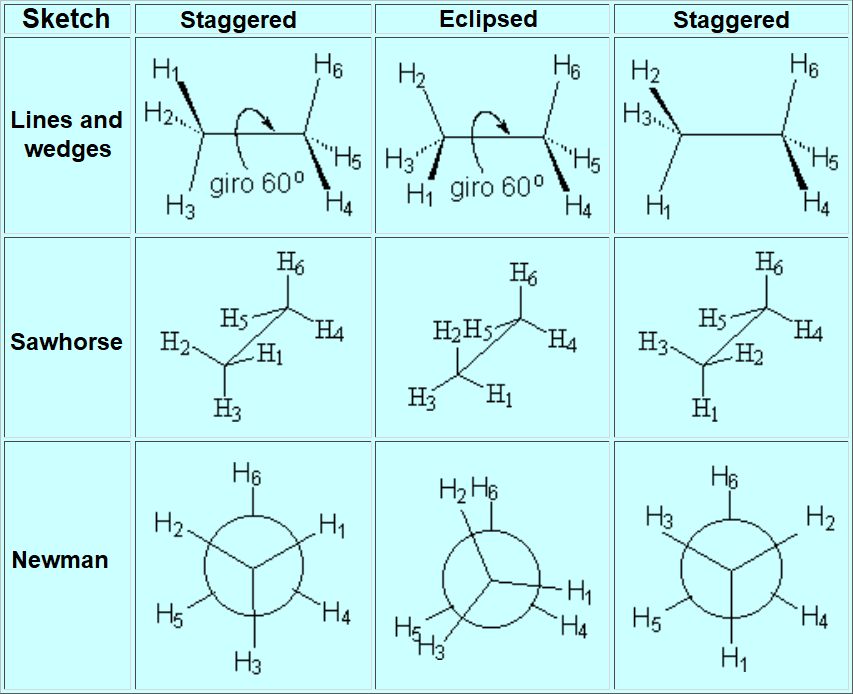
The most practical and visual way of representing conformations is the so-called NEWMAN PROJECTION
Melvin S. Newman (1908-1993): Professor at the University of Ohio (USA). His research delt with the steric effects in congested molecules. He made important contributions to reaction mechanisms and to the chiral properties of numerous molecules. His teaching abilities were outstanding and, among many other things, he proposed the popular projection, named after him, used to easily represent conformations in organic compounds.
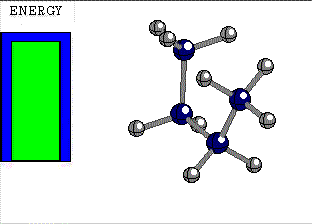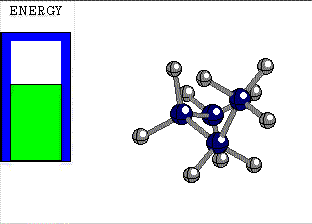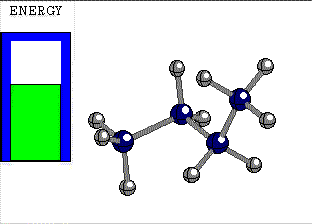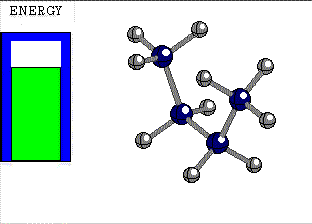
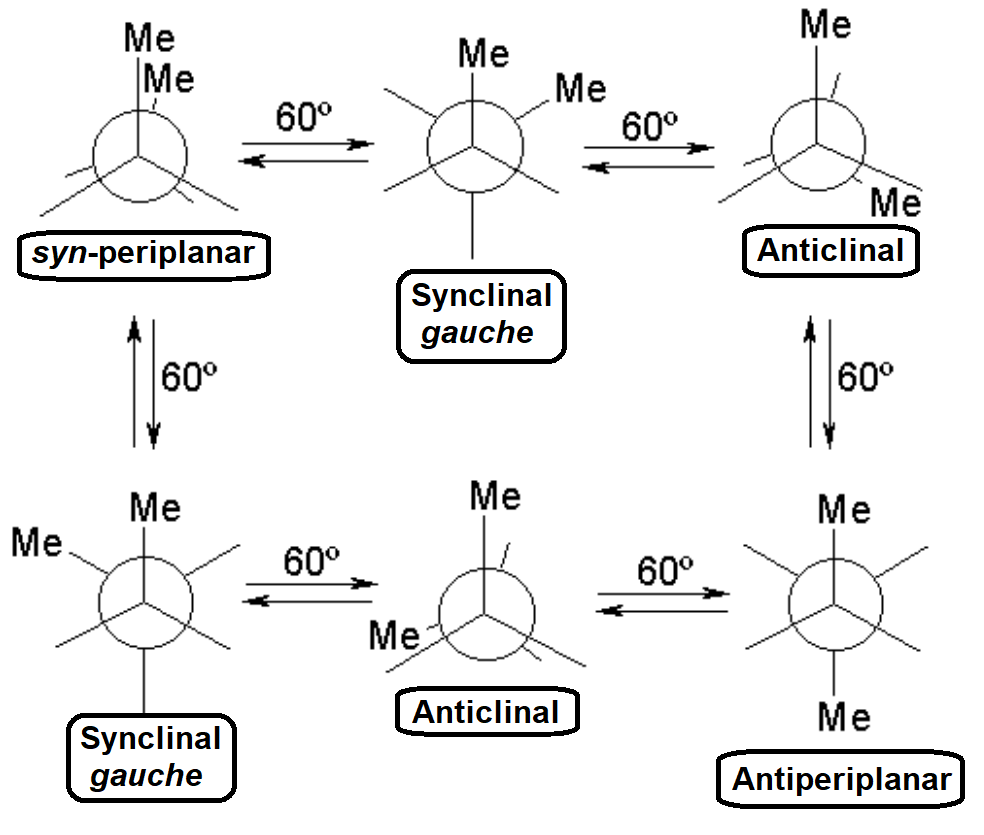
 STAGGERED
STAGGERED
 ECLIPSED
ECLIPSED
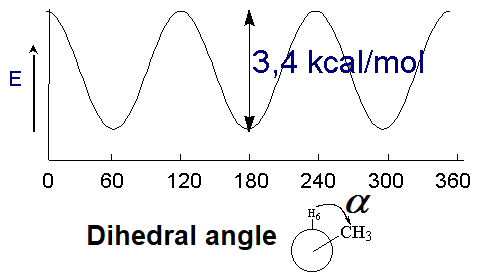
Even though the overlapping of orbitals is not affected by their twisting, the rotation of a single bond has indeed an energy cost, yet very small, that depends on the size of the groups attached to the rotating atoms.
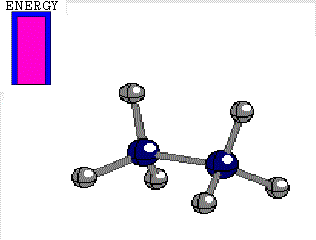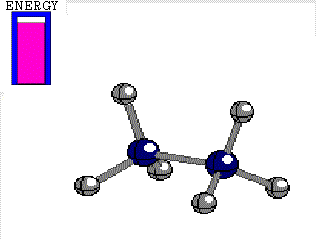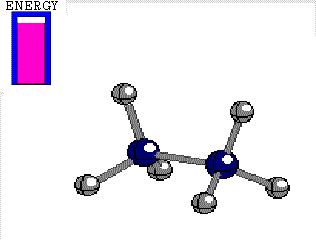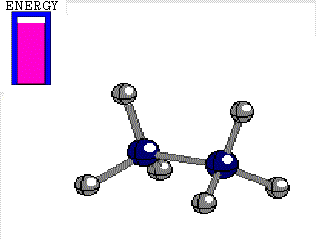 Energy difference between the alternated and eclipsed conformations of ethane
Energy difference between the alternated and eclipsed conformations of ethane
(3 kcal/mol)
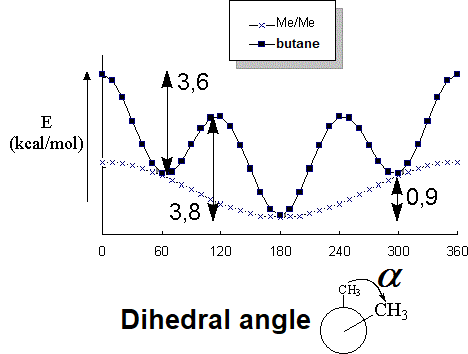
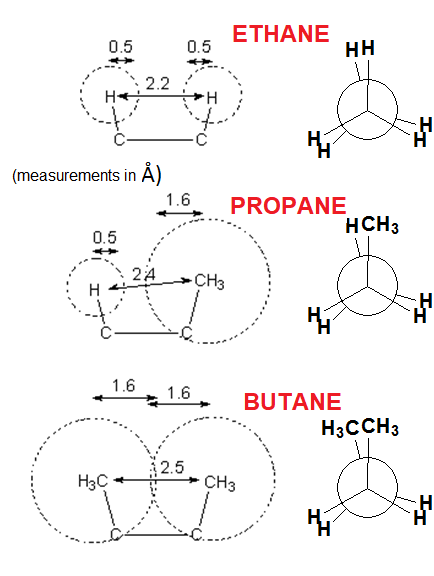
How would the energy profile be in PROPANE for the C-C bond rotation?
And for the central C-C bond in BUTANE?
The most important factor creating the barrier to rotation of a single bond is the STERIC INTERACTION of the flanking hydrogens in the eclipsed conformation.
A methyl group is larger than a hydrogen and the steric interaction in propane and butane is bigger, thus making the energy barrier higher.
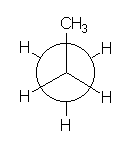 PROPANE
PROPANE
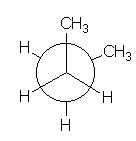 BUTANE
BUTANE
In BUTANE, the energy difference between the lowest energy minimum (rotamer with the antiperiplanar methyls at 180º each other) and the other local minima (rotamers with the gauche methyls at 60º and 300º) is 0.9 kcal/mol.
This is the energy (0.9 kcal/mol) that measures the destabilizing interaction between two methyl groups in gauche arrangement.
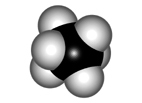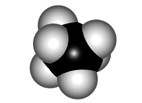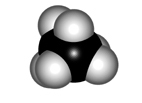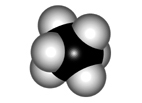

 STAGGERED
STAGGERED
 ECLIPSED
ECLIPSED
 Energy difference between the alternated and eclipsed conformations of ethane
Energy difference between the alternated and eclipsed conformations of ethane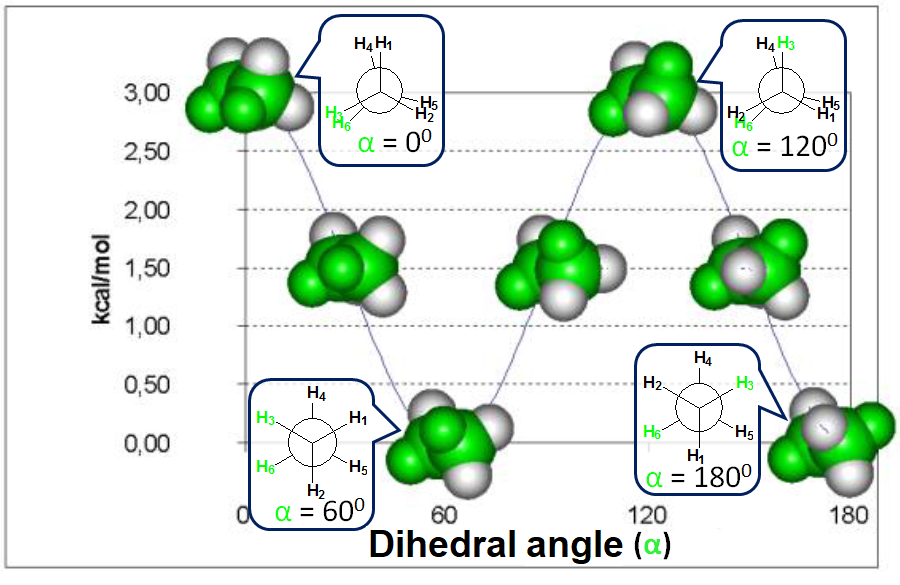
 PROPANE
PROPANE
 BUTANE
BUTANE