NUCLEI ALIGNMENT WITH AN EXTERNAL MAGNETIC FIELD
Magnetic-moment bearing nuclei, like 1H and 13C, become interesting when one places them in an intense magnetic field (Ho or Bo).
Do you remember how a compass works?
It consists of a magnetic needle which is influenced by the earth's magnetic field. The needle aligns with the magnetic north pole, doesn't it?
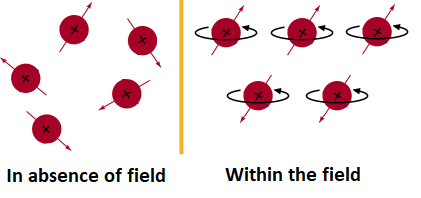 Nuclei magnets in the presence or absence of an external magnetic field.
Nuclei magnets in the presence or absence of an external magnetic field.
It similarly happens to magnetic nuclei, although observing the effect requires a much stronger magnetic field than earth's.
Nuclei in the intense magnetic field Ho behave similarly to the compass' needle with a difference: nearly half of the nuclei align as much as they can with the field's north pole and the other half, with the field's south pole. Let me insist: 'as much as they can' or better said, as much as quantum mechanics allow them.
Prior to being under the influence of the magnetic field, the nuclei bore all the same energy and random orientations. When immersed in it, they split in two groups of different orientation, (+z) and (-z), and acquire different energies, one group being slightly more stable and slightly more populated than the other.
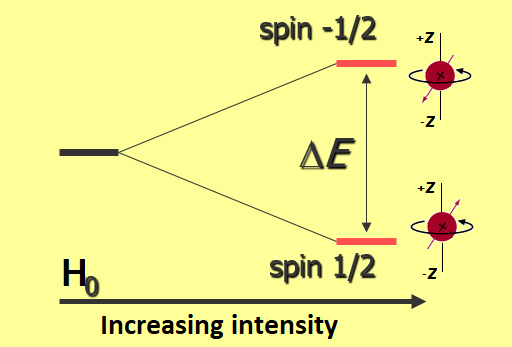 Separation of nuclei into two levels of energy due to the external magnetic field.
Separation of nuclei into two levels of energy due to the external magnetic field.
Considering again the methane molecule within the magnetic field, remember 99% of 12C(1H)4 plus 1% of 13C(1H)4, have the four equivalent 1H split into two groups, one group pointing to (+z) axis and the other to (-z) axis, the two of them separated by a certain amount of energy.
Besides from that, the 1% of 13C(1H)4 have their 13C atoms divided as well into two groups, one group pointing to (+z) axis and the other to (-z) axis, the two of them separated by a certain amount of energy.
You may wonder:
How much is that energy difference?
Is the energy difference the same for 1H and 13C?
The Plank-Einstein (E = h·'nu') and Larmor equations ('nu'='gamma'·Ho/2·'pi') give us the answer.
It can be seen that the energy difference is directly proportional to the strength of the external magentic field (H0). The higher its strength, the larger the separation in energy between the nuclei aligned to (+z) and (-z) axis and the larger the population difference.
In the second place, the separation depends on a constant belonging to each nucleus, the gyromagnetic constant ('gamma'), whose value for 1H is approximately four times that of 13C.
Therefore, for the same strength of Ho, separation between energy levels is for 1H four times as much as that for 13C.
Using specific numbers, for a moderate external magnetic field (H0) of 18100 gauss (1.81 Tesla), the resonance frequency is
'nu' = 80 MHz for 1H and 20 MHz for 13C.
The resonance frequency for 1H is thus four times as much as for 13C because the gyromagnetic constant of 1H is four times as much as that of 13C.
For that particular value of H0, the energy difference between levels either for 1H (5.3·10^-26 j) or 13C (1.3·10^-26 j) is tiny. Again, that of 13C is four times lower than that of 1H as explained because of the different gyromagnetic constant.
As if it were a miracle, the enormous power of NMR spectroscopy in structural determination depends on these tiny, minute energy differences.
 Nuclei magnets in the presence or absence of an external magnetic field.
Nuclei magnets in the presence or absence of an external magnetic field.
 Separation of nuclei into two levels of energy due to the external magnetic field.
Separation of nuclei into two levels of energy due to the external magnetic field.
